Axell AI Contest 2024 技術解説

1 はじめに

先日開催された学生対象のAIモデル開発コンテスト『Axell AIContest 2024』で2位となった解法を紹介します。このコンテストの課題は「高速」かつ「高精度」な画像超解像モデルを開発するというものでした。コンテストの詳細についてはSIGNATEのコンテストページをご参照ください。抜粋すると、コンテストのルールは次のとおりです。

1. 入力画像を4倍にする超解像モデルの開発（提出フォーマットはONNXモデル）
2. Tesla T4相当のHWを用いて、60fpsの動画（1024×1024）をリアルタイムに4096×4096に超解像処理できる程度の処理速度
3. githubなどで公開されている（論文などの）学習済みモデルを利用しても良い
4. 訓練データ・検証データは配布される。ただし各自で追加のデータセットを用いても良い。テストデータは未公開
5. モデルの性能はPSNRで評価

特に処理速度の制約が厳しく、既存の超解像モデルをそのまま利用すると上記のルール2を満たすことができません。そこで既存の超解像モデルは利用せず、いくつかの要素技術を活用してオリジナルの超解像モデルを作成しました。また、データセットを増やすと1回の学習に要する時間が伸び、コンテスト期間中に試行錯誤できる回数が減ると判断し、提供されたデータセットのみを利用しました。なお以下で紹介する各要素技術については、コンテスト期間の制約や1日に投稿できるモデル数に上限があったため、きちんとAblation Studyしたわけではありません。そのため、それぞれの技術が精度にどの程度寄与しているか断定できないという点はご了承ください。

2 解法

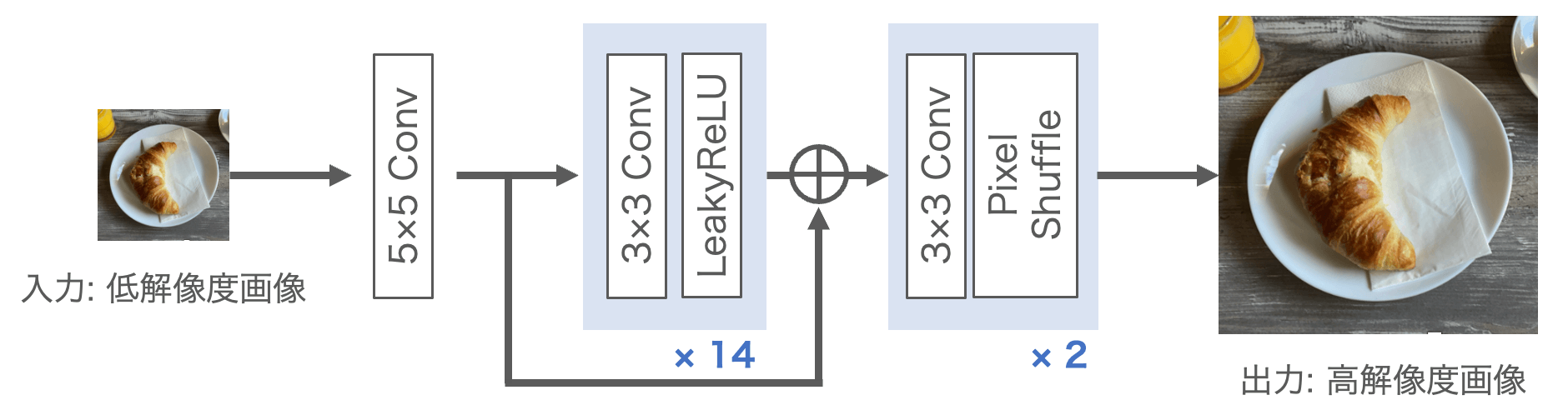
推論時のネットワーク構造を図1に示します。17層の畳み込み層からなるネットワークで、1つだけshortcut connectionがあるというごく単純なモデルです。以下で今回用いた要素技術について実装方法とあわせて紹介します。なお実装にはPyTorchを用いました。

2.1 半精度化

PyTorchでモデルを作成すると、特に指定しない場合にはFP32で演算が行われます。しかしFP32で演算を行いつつコンテストで求められている処理速度を満たそうとした場合、チャネル数にもよりますが5層前後の畳み込み層しか利用することができません。ニューラルネットワークは多層化することで性能を発揮すると言われていますので、層を増やすために半精度化を行いました。半精度化とは、入力データと学習済みモデルのデータ型をFP16に変換することです。FP16で演算することでFP32で演算する場合よりも高い並列度で計算できるようになるため、高速に処理することができるようになります。

さらに、今回のコンテストのテスト環境で用いられるTesla T4はTuring Tensorコアが搭載されているため、低精度化によって処理速度が大幅に向上します。NVIDIAのHPによると、Tesla T4のFP32のパフォーマンスは8.1TFLOPS、FP16のパフォーマンスは65TFLOPSであり、理論値で約8倍の高速化が期待できます（実際には8倍も速くならない場合もあります）。Turing Tensorコアなど低精度向けのコアを内蔵していないGPUを用いてFP16による演算を行う場合には、Tesla T4よりもハイエンドなGPUであってもTesla T4よりも推論速度が劣ることがあります。
学習済みモデルを半精度化するPyTorchコードをプログラム1に示します。forwardメソッドの冒頭にX_in = X_in.half()を追記して入力データをFP16に変換しています。また本コンテストの提出モデル形式がONNXであったため、ONNXモデルに書き出しています。ONNXモデル書き出し時にmodel.half()とすることでモデルパラメータをFP16に変換しています。なお入力データとモデルパラメータのデータ型が異なるとエラーが発生するので注意してください。

プログラム1: 学習済みモデルの半精度化

import torch
from torch import nn
class MySRModel(nn.Module):
  def __init__(self) -> None:
    super().__init__()
    # 省略
  
  def forward(self, X_in: tensor) -> tensor:
    X = X_in.half()
    # 省略
    return X

if __name__ == "__main__":
  model = MySRModel()
  model.load_state_dict(torch.load("<path_to_trained_model>.pth"))
  torch.onnx.export(model.half(), dummy_input, f"<path_to_save_dir>/model.onnx",
    opset_version=17,
    input_names=["input"],
    output_names=["output"],
    dynamic_axes={"input": {2: "height", 3:"width"}})

2.2 Re-parameterization

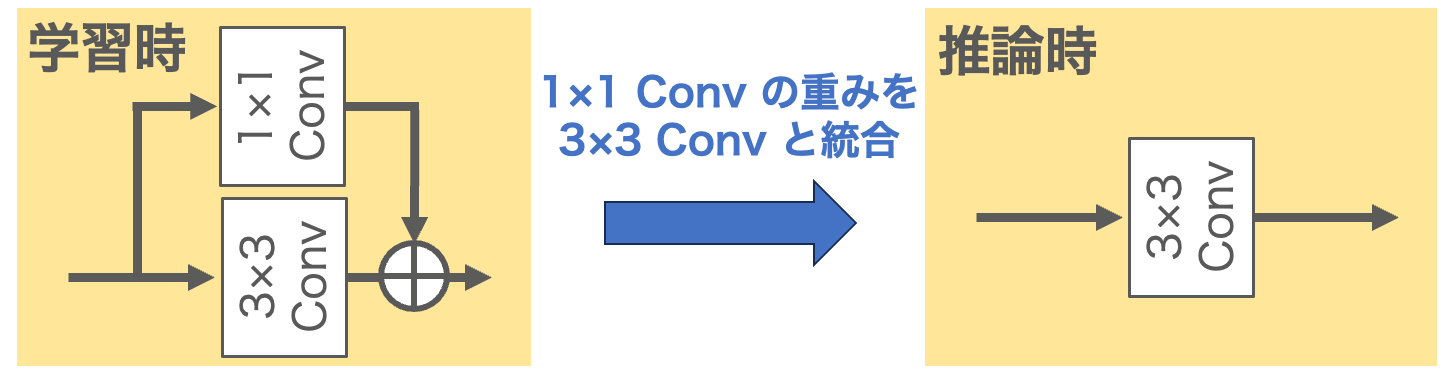
追加の計算コストを必要とせずに精度を向上させるために、re-parameterizationを全ての3×3畳み込み層に適用しました。Re-parameterizationとは、ここでは計算結果は変えずにより低コストな計算手順になるようモデルパラメータを変更することをいいます。今回は、図2に示すように学習時にはカーネルサイズが3×3のものと1×1のものを並列に適用して出力を足し合わせるような構造にしておき、推論時にはカーネルサイズ1×1の重みを3×3の方にマージするようなre-parameterizationを適用しました。これにより、学習時にはネットワークにより高い表現能力を持たせることができます。

もう少し詳しく説明します。カーネルサイズ3×3のフィルタ（カーネル）を用いて1回の畳み込み演算を行う場合のフィルタの重みを \(\mathbf{w}_{i,j}\), 入力を \(\mathbf{a}_{i,j}\) とすると、出力 \(o\) は次の式で表されます（※ \(\mathbf{w}_{i,j}\) と \(\mathbf{a}_{i,j}\) はともに入力チャネル数分だけの次元を持つベクトルです）。

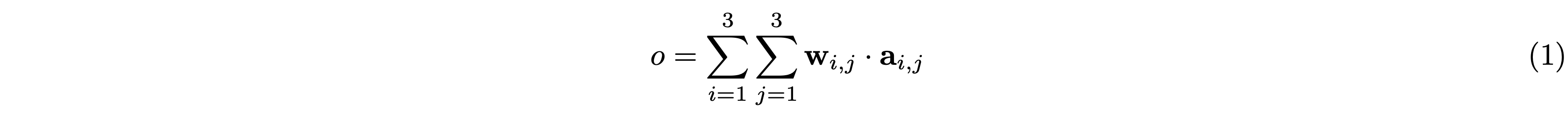
同様に、カーネルサイズ1×1のフィルタを用いた1回の畳み込み演算の出力 \(o’\) は、フィルタの重みを \(\mathbf{w}’\) として次の式で表されます。

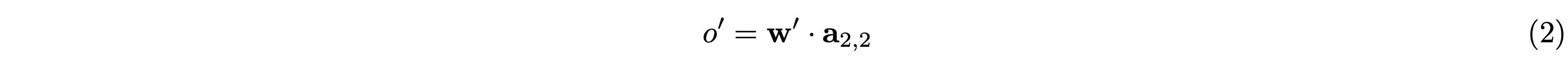
したがって、カーネルサイズが3×3のものと1×1のものを並列に適用して出力を足し合わせた場合の出力は次のようになります。

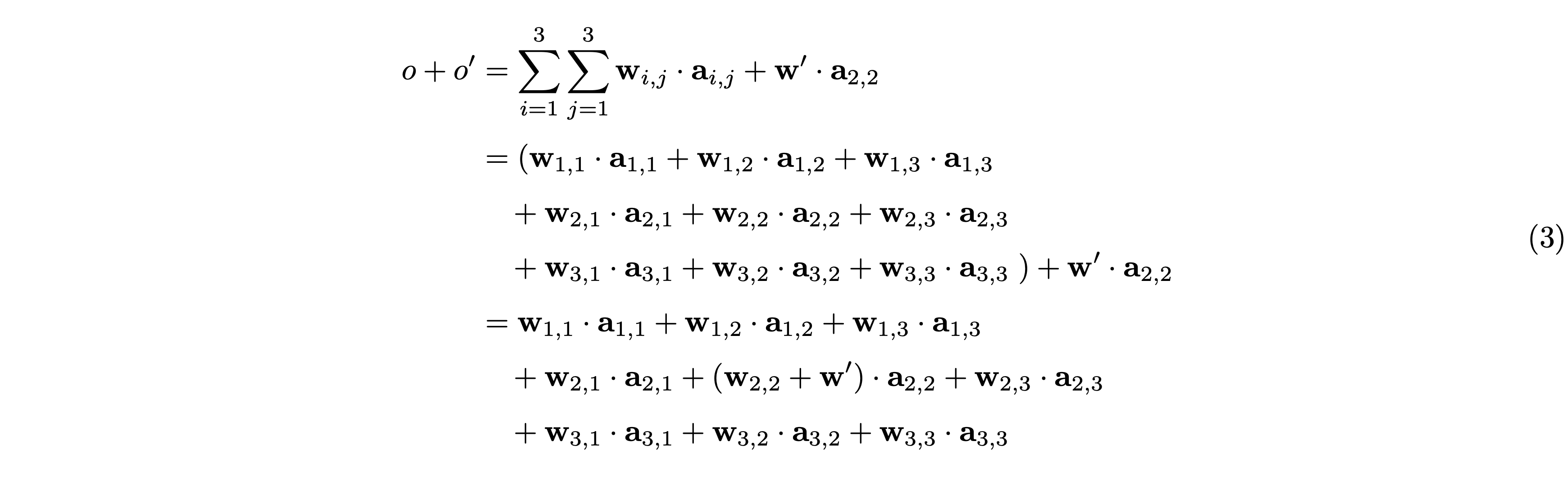
ゆえに、推論時には1×1畳み込み層の重み \(\mathbf{w}’\) を3×3畳み込み層の重み \(\mathbf{w}_{2,2}\) に事前に足し合わせておくことで、3×3畳み込み層1回の計算コストで、カーネルサイズが3×3、1×1の2つの畳み込み層を並列に適用して出力を足し合わせた場合と同じ計算結果を得ることができます。バイアス項も学習させる場合には、2つの畳み込み層で共通のバイアス項を持たせて学習すれば良いでしょう。
Re-parameterizationのPyTorch実装をプログラム2に示します。訓練時には単にconv = RepBlock(3,64)のように利用し、学習を終えた後にconv = conv.reparameterize()とすることで、1層の3×3畳み込み層に変換できます。なお、私はもともとre-parameterizationの実装方法を知りませんでしたので、ChatGPTに「PyTorchでの3×3 Convと1×1 Convのre-parametrizationの実装方法を教えてください。」と質問して教えてもらいました（プログラム2はChatGPTが出力してくれたコードです）。

プログラム2: Re-parameterization

import torch
from torch import nn
from torch.nn import functional as F
class RepBlock(nn.Module):
  def __init__(self, in_channels, out_channels):
    super(RepBlock, self).__init__()
    self.conv3x3 = nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1, bias=False)
    self.conv1x1 = nn.Conv2d(in_channels, out_channels, kernel_size=1, padding=0, bias=False)
    self.bias = nn.Parameter(torch.zeros(out_channels))
  
  def forward(self, x):
    return self.conv3x3(x) + self.conv1x1(x) + self.bias.view(1, -1, 1, 1)

  def reparameterize(self):
    weight3x3 = self.conv3x3.weight.data
    weight1x1 = F.pad(self.conv1x1.weight.data, [1, 1, 1, 1])
    reparam_weight = weight3x3 + weight1x1
    reparam_bias = self.bias.data
    reparam_conv = nn.Conv2d(self.conv3x3.in_channels, self.conv3x3.out_channels, kernel_size=3, padding=1, bias=True)
    reparam_conv.weight.data = reparam_weight
    reparam_conv.bias.data = reparam_bias
    return reparam_conv

2.3 Weight Normalization

ネットワークを多層化すると学習が不安定になります（勾配消失/爆発問題）。学習を安定化させる代表的な手法としてはBatch Normalizationなどの正規化層を追加することが挙げられます。しかし、超解像タスクにおいては正規化層を用いると精度低下につながることが知られています[1]。論文などで用いられている超解像ネットワークは密なshortcut connectionを持つネットワーク（DenseNet[2]など）が主に用いられているために、正規化層を用いなくとも比較的学習が安定するのだと思われます。今回は、正規化層を追加したりshortcut connectionを増やすことなく、学習を安定化させるWeight Normalization[3]という手法を全ての畳み込み層に適用しました。
Weight Normalizationは各層の重み \(\mathbf{w}\) をスケール \(g\) と方向 \(\mathbf{v}\) に分けて扱う手法です。

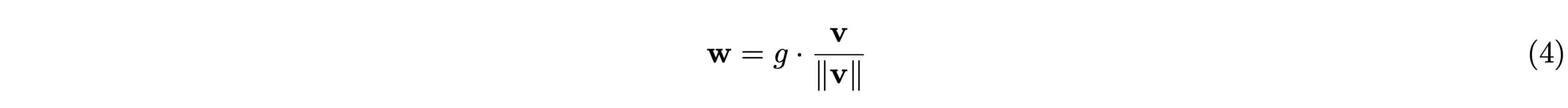
Weight Normalization適用前と適用後では、順伝播の計算結果は変わりませんが、逆伝播時の勾配が変化します。論文[3]より、逆伝播時の \(g\) と \(\mathbf{v}\) に対する損失関数 \(L\) の勾配はそれぞれ次のようになります。

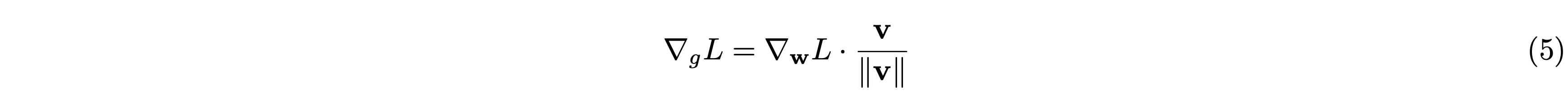
ここで \(I\) は単位行列です。\(\dfrac{\mathbf{w}\mathbf{w}^{\top}}{\|\mathbf{w}\|^2}\) は \(\mathbf{w}\) 方向への射影行列を表しています。そのため、行列 \(M_{\mathbf{w}}\) では \(\mathbf{w}\) と直行する成分を計算します。
ニューラルネットワークの学習は勾配の共分散行列が単位行列に近いほど安定するそうです。重み \(\mathbf{v}\) に関する勾配の共分散行列 \(D\) は次のように表せます。

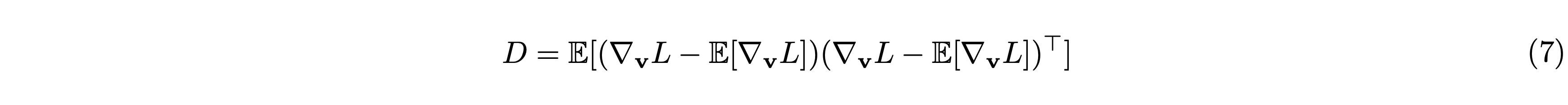
\(\mathbb{E}\) は期待値を表します。今はある特定の \(\mathbf{w}\) について議論していますので、\(\mathbb{E}\left[M_{\mathbf{w}}\right]\) は固定値（\(=M_{\mathbf{w}}\)）です。よって \(\nabla_{\mathbf{v}}L – \mathbb{E}[\nabla_{\mathbf{v}} L]\) は次のように表せます。

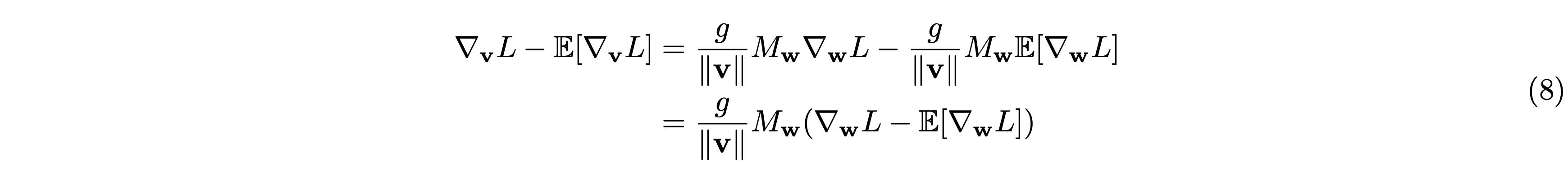
したがって \(D\) は次のように変形できます。

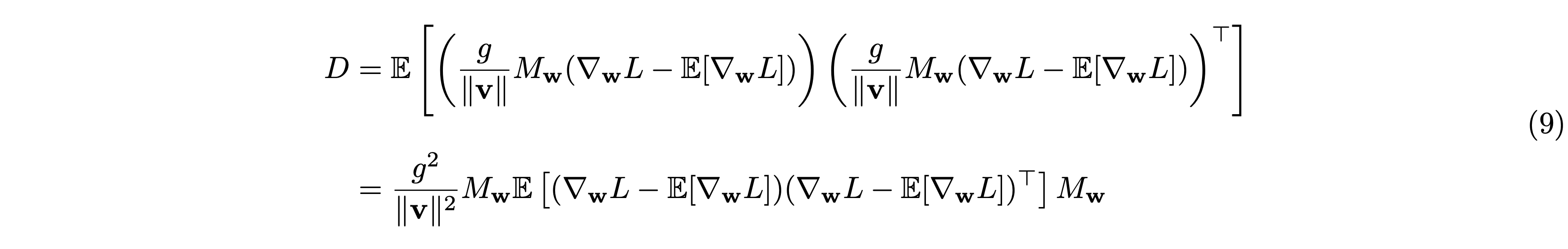
ここで、重み \(\mathbf{w}\) に関する勾配の共分散行列 \(C\) は次のように表せます。

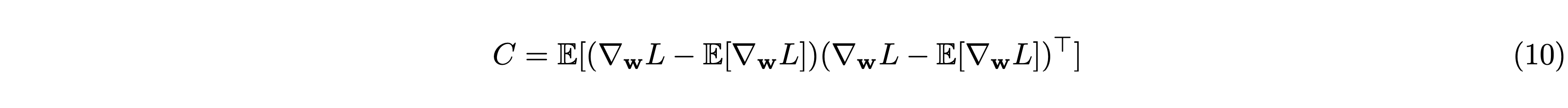
ゆえに \(D\) は \(C\) を用いて次のように表せます。

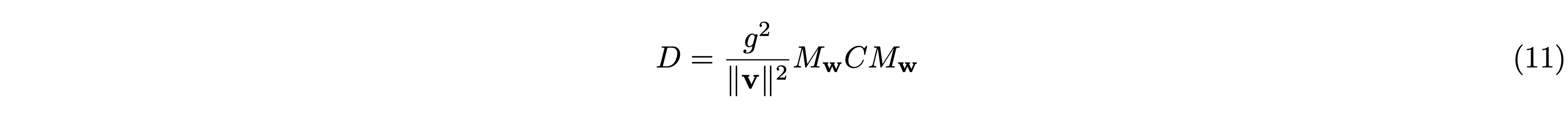
共分散行列 \(C\) の支配的な固有ベクトル（最大固有値に対応する固有ベクトル, dominant eigenvector）は \(\mathbf{w}\)（または \(\mathbf{w}\) に近いベクトル）であることが多いようです。\(M_{\mathbf{w}}\) は\(\mathbf{w}\) の補空間への射影行列ですので、共分散行列 \(D\) は \(C\) よりも単位行列に近くなり、学習が安定化します。
また、学習時に \(\mathbf{v}\) は自身と直交する方向に更新されますので、三平方の定理より \(\mathbf{v}\) のノルム（ベクトルの長さ）は次第に大きくなります。\(\mathbf{v}\) の勾配は \(g/\|\mathbf{v}\|\) でスケーリングされるため、仮に大きな学習率を使用した場合であっても比較的学習が安定します（学習率が大きいと \(\mathbf{v}\) のノルムが早い段階で大きくなり、その分 \(1/\|\mathbf{v}\|\) は小さくなります）。
Weight NormalizationのPyTorch実装をプログラム3に示します。実装は容易で、weight_norm関数でWeight Normalizationを適用、remove_parametrizations関数でWeight Normalizationを外すことができます。推論時にはWeight Normalizationは不要なので、学習が終わった後は外しておくと良いでしょう。なお今回学習させたネットワークはWeight Normalizationを適用しない場合には損失が途中でnanになってしまい、学習が行えませんでした。

プログラム3: Weight Normalization

from torch import nn
from torch.nn.utils.parametrizations import weight_norm
from torch.nn.utils.parametrize import remove_parametrizations

conv = nn.Conv2d(3, 64)
conv = weight_norm(conv) # Weight Normalization を適用
remove_parametrizations(conv, "weight") # Weight Normalization を外す

2.4 損失関数

学習時の損失関数 (\(L\)) には、L1 Loss (\(L_{l1}\))とGradient Variance Loss (\(L_{GV}\))[4]を併用しました。

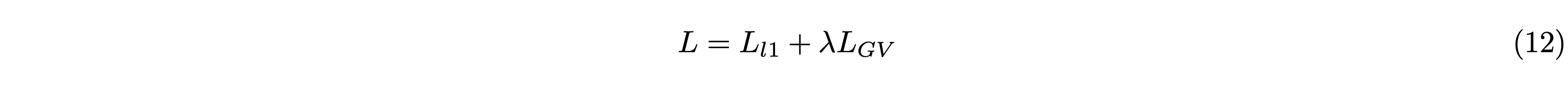
\(\lambda\) はGradient Variance Lossの重み係数です。Gradient Variance Lossの定義は次のとおりです。

ここで \(v_{x}^{SR},\,v_{x}^{HR}\) はそれぞれ超解像画像の勾配マップと正解画像（高解像度画像）の勾配マップにおけるx方向の勾配の分散を表します。同様に、\(v_{y}^{SR},\,v_{y}^{HR}\) はy方向の勾配の分散を表します。超解像画像（SR）と正解画像（HR）のx,y方向の勾配マップ \(G_x^{SR},\,G_y^{SR},\,G_x^{HR},\,G_y^{HR}\) を得るために、RGB画像をグレースケールに変換してSobelフィルタを適用します。次にこれらを \(n\times n\) のパッチに分割し、各パッチをベクトル化します。ベクトル化したものを \(\tilde{G}_x^{SR},\,\tilde{G}_y^{SR},\,\tilde{G}_x^{HR},\,\tilde{G}_y^{HR}\) とすると（それぞれ \(n^2 \times (w\cdot h/n^2)\) の次元を持つ行列です）、各パッチの分散 \(v_{i}\) は次のように計算されます。

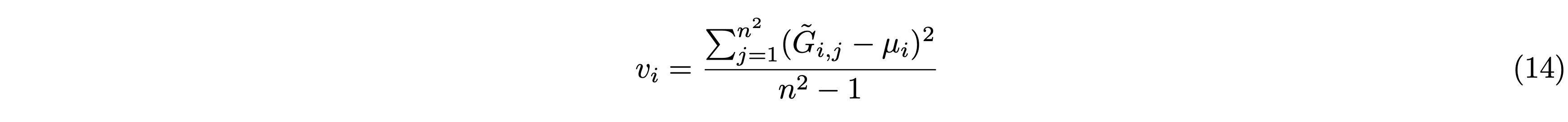
ここで \(\mu_{i}\) はパッチ \(i\) の平均値を表します。Gradient Variance Lossは、特に超解像画像のエッジの鮮明さを向上させる働きをします。今回は、係数 \(\lambda\) は0.01、パッチサイズ \(n\)は16としました。
勾配マップ（Sobelフィルタ適用結果）と勾配分散（Gradient Variance）を可視化した例を図3に示します。それぞれ画像のエッジ部分が白く、そうでない領域は黒くなっているのがわかります。実装については公式のgithubリポジトリにあるgradient_variance_loss.pyを利用すればOKです。criterion_gv = GradientVariance(patch_size=16)のように利用します。

2.5 Optimizer

OptimizerにはRAdamにLookahead[5]を組み合わせたものを用いました。RAdam+Lookaheadの組み合わせのことをRangerと言うそうです。ニューラルネットワークの訓練にはOptimizerとしてAdamやその派生版がよく利用されています。スコアを競うコンテストなのでOptimizerによって精度が変わるのであればできるだけ良いものを利用したいですが、Optimizerを変更した場合の比較実験までやっている余裕はありませんでした。ですので、「これを使っておけば問題ないだろう」というRAdam+Lookaheadを採用しました。LookaheadはN回重みを更新した後に、過去の重みと現在の重みを補間した間の重みを採用する、というものです。
最適化手法の理論は専門外なので詳細には立ち入らず、ここでは使い方のみ紹介します（プログラム4）。Lookaheadの実装は公式のgithubリポジトリにあるlookahead_pytorch.pyを利用すればOKです。Lookaheadの引数には、Optimizer（ここではRAdam）、la_steps、la_alphaを指定します。la_stepsは何回重みを更新したら前回記録した重みと現在の重みを補間するのかを表し、la_alphaは補間する際の係数を表します。la_alphaに1を指定した場合にはLookaheadを用いない場合と同じ挙動になります。また、推論時（学習中の検証データを用いた評価時）やモデル保存時には前回記録した重みを用います。このために_backup_and_load_cache()を呼び出しています。学習に戻る際には_clear_and_load_backup()を呼び出します。

プログラム4: Optimizer

from torch.optim import RAdam
from lookahead_pytorch import Lookahead

# Optimizer の作成
optimizer = RAdam(model.parameters(), lr=learning_rate)
optimizer = Lookahead(optimizer=optimizer, la_steps=5, la_alpha=0.8)

# 推論やモデル保存時
optimizer._backup_and_load_cache()
## (ここで推論や保存)
optimizer._clear_and_load_backup()

3 学習させたネットワークの分析

学習させたネットワークについて、どのように高解像度画像を推定しているのか分析してみます。図4に示すように、shortcut connection側の経路を通るオレンジ色の部分の処理には活性化関数が含まれていませんので、入力画像に対して線形変換のみ行われます。また、畳み込み層の層数も入力層と出力層側2層の計3層のみなので、この経路では比較的早く学習が進むと考えることができます。反対に、shortcut connection側の経路を通らない中間層では非線形変換が行われます。層数も14層あるので、shortcut connection側の経路に比べれば学習はゆっくり進むと考えられます。これらのことから、shortcut connection側の経路では高解像度画像のうちの低周波成分が、もう一方の中間層を経由する経路では高周波成分が推定されると考えられます。

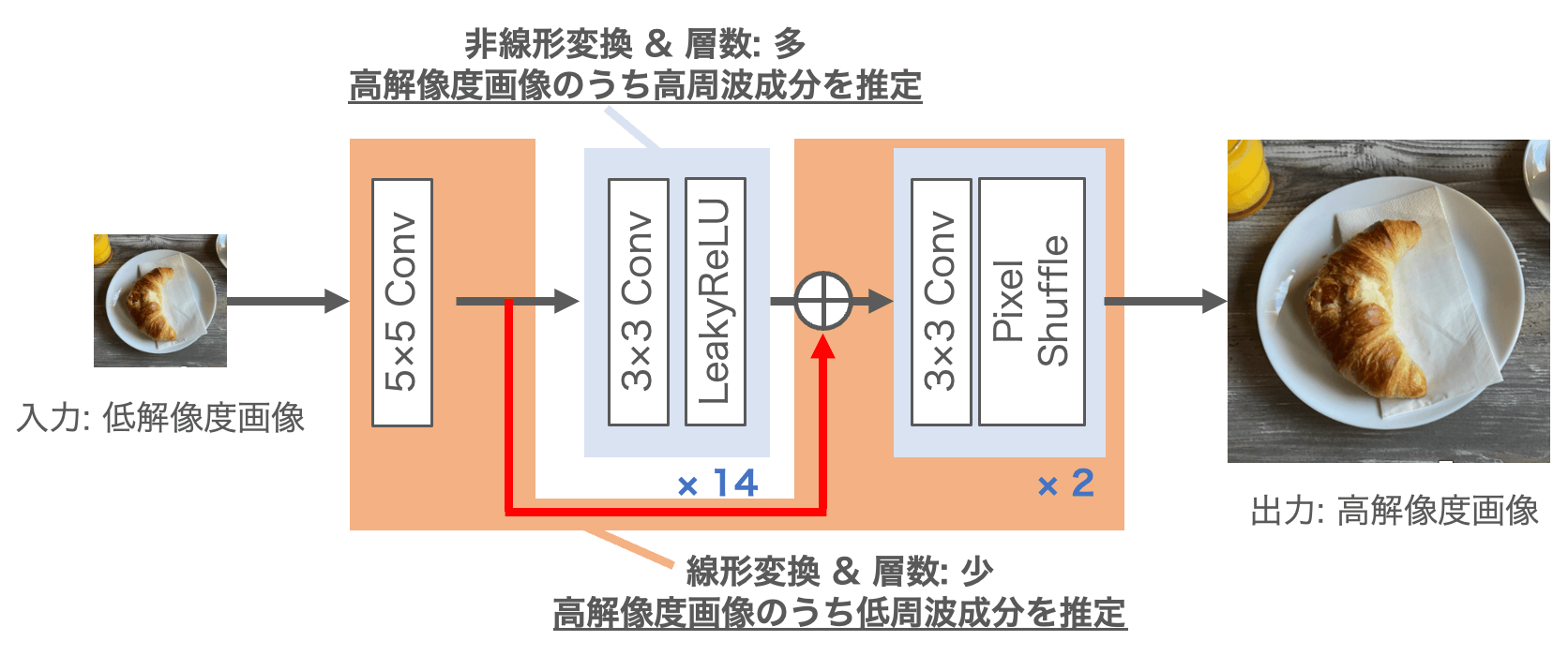
このことを確かめるために、実際にshortcut connection側の経路の層のみを用いた場合の出力画像と、shortcut connectionを外した場合の出力画像を確認してみました。結果を図5に示します。どうやら実際にそのような推定がなされているようです。また、shortcut connectionを外した場合の出力画像で相対的に画素値が大きい領域は、勾配分散の値が大きい領域と対応しているように思われます。つまり、学習時のGradient Variance Lossは中間層の学習に寄与していると解釈することもできそうです。

参考文献

1. Bee Lim, Sanghyun Son, Heewon Kim, Seungjun Nah, and Kyoung Mu Lee. Enhanced deep residual networks for single image super-resolution. In 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), pp. 1132–1140, 2017.
2. Gao Huang, Zhuang Liu, Laurens van der Maaten, and Kilian Q Weinberger. Densely connected convolutional networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 2261–2269, 2017.
3. Tim Salimans and Diederik P. Kingma. Weight normalization: a simple reparameterization to accelerate training of deep neural networks. In Proceedings of the 30th International Conference on Neural Information Processing Systems (NeurIPS), pp. 901–909. Curran Associates Inc., 2016.
4. Lusine Abrahamyan, Anh Minh Truong, Wilfried Philips, and Nikos Deligiannis. Gradient variance loss for structure- enhanced image super-resolution. In Proceedings of the International Conference on Acoustics, Speech and Signal Processing (ICASSP), pp. 3219–3223. IEEE, 2022.
5. Michael R. Zhang, James Lucas, Geoffrey Hinton, and Jimmy Ba. Lookahead optimizer: k steps forward, 1 step back. In Proceedings of the 33rd International Conference on Neural Information Processing Systems (NeurIPS), pp. 9593–9604. Curran Associates Inc., 2019.